树状数组与“分块”

分块是一种常见的数据结构，通常我们按 $\sqrt n$ 为块长来分块，以获得 $O(n\sqrt n)$ 的时间复杂度。

当然，这里不是指一般所说的根号分块，而是一种针对向下取整运算的技巧~~

下面我们结合一道例题来看看这是什么意思：

已知长为 $n$ 的序列 $A$ 和一个长为 $n-1$ 的序列 $T$。给定 $K,D$，求满足以下递推式的 $dp$ 数列的每一项：

数据范围：

• $K\leq n\leq 2\times 10^6$，
• $D\in[-10^{10},10^{10}]$，
• $\forall i\in[1,n],A_i\in[-10^{10},10^{10}]$，
• $\forall i\in[1,n-1],i<T_i\leq n-i$，
• 所有输入都是整数。

初步思考

一个简单的思路是 $O(n^2)$ 暴力，实现极为简单。继续深入一下我们发现最难搞的就是那个向下取整的部分：$\lfloor\frac{j-i}{K}\rfloor\cdot D$，由于这个函数与 $j$ 并未构成双射，我们不能够逆推快速得到答案。我们令 $f(j)=\lfloor\frac{j-i}{K}\rfloor\cdot D$，当务之急，就是处理这玩意。

另外，注意到数据范围，应该比较卡常，因此要用小常数的数据结构。比如树状数组或者二分。

方法一

注意到向下取整部分的分母 $K$ 是个常数，在单独求解 $dp_i$ 的过程中， $i$ 又可以看做常数，这意味着 $j$ 每增加 $K$，$f(j)$ 才增加 $1$。

也就是说，从 $i$ 开始每 $K$ 个数，$f(j)$ 都是一样的，那么可以批量处理！也就是把这 $K$ 个数当做一块统一处理。

目前思路便有点清晰了。我们来手动模拟一下。

模拟过程

显然，我们没有必要模拟整个过程，而只需要考虑其中的一次转移即可。

下面，我们来模拟一遍 $n=16,K=3,D=4$，$A=(9,9,8,2,4,4,3,5,3,-1,-1,4,-5,-1,5,9)$，$T=(1,2,3,4,5,3,7,4,2,1,1,3,3,2,1)$ 的情况。

以 $i=7$ 为例：

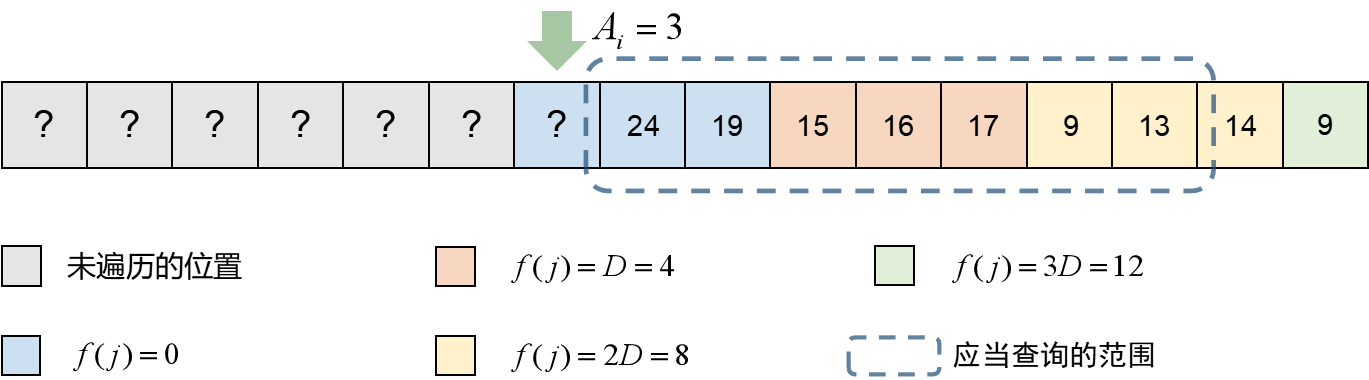
实际上绿色箭头所指的地方（第 $i=7$ 个位置）可以纳入考虑，而不影响答案。大概就是这样：

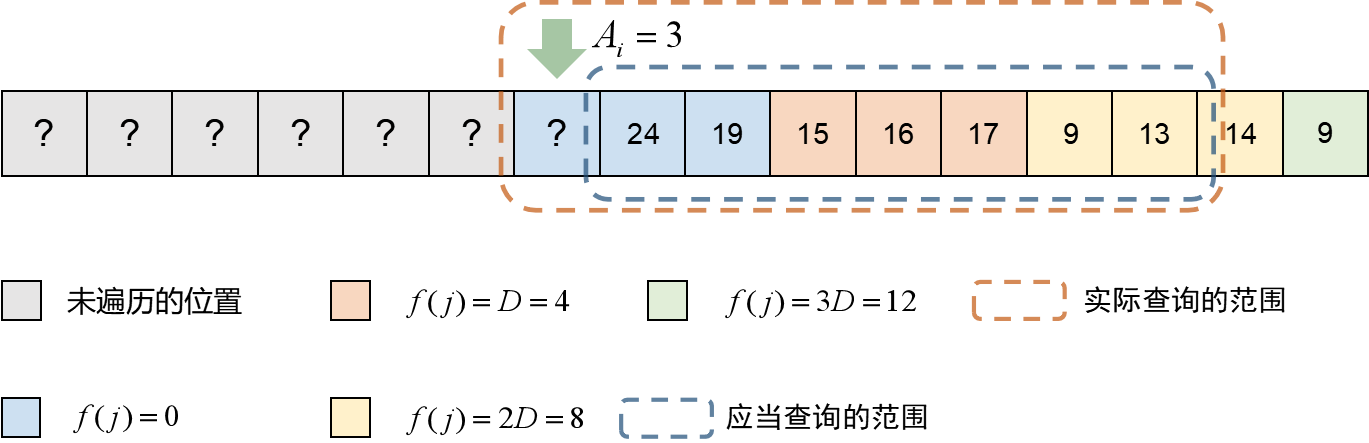
可以发现这里其实选 $j=8$ 即可得到最佳答案，问号处应该填 $27$。

分析过程

我们发现查询的东西仅由两个部分构成：

1. 若干个完整的长为 $K$ 的块；
2. 一个块的前缀。

设有 $m$ 个块，第 $j$ 个块内的最大值是 $p_j$，那么第 1 部分的贡献就是：$\max\limits_{1\leq j \leq m}\{ p_j-(j-1)D\}$；

设最后一段从 $u$ 开始，到 $v$ 结束，是从 $i$ 开始的第 $w$ 块，那么第二部分的贡献是：$\max\limits_{u\leq j \leq v}\{dp_j-(w-1)D\}$。

我们发现整块的信息可以 $O(n)$ 的空间复杂度储存！也就是，对每个 $i$ 到 $i+K-1$，记录它们中 $dp$ 的最大值，存在数组 $p_i$ 中。那么要知道从 $i$ 开始的块的贡献，只需要查 $p_i$ 就可以了。

接下来我们思考如下问题：

1. 尽管信息存下来了，如何查询部分 1？
2. 不是有一个增量 $D$ 吗？每一段的 $D$ 的系数不一样，怎么解决呢？
3. 部分 2 怎么求答案？
4. 如何维护 $p$ 与 $\rm BIT$？

问题 1

如之前的图所示，当查询 $i$ 的时候，只有 $j\bmod K=i$ 的 $p_j$ 才会被查到。因此我们开 $K$ 个树状数组（$\rm{BIT}$），编号从 $0$ 到 $K-1$。编号为 $i$ 的存 $p_j,\ s.t.\ j\bmod K=i$ 的前缀最大值，每个树状数组大小是 $O(\frac nK)$，这样总空间复杂度是 $O(n)$ 的。

尽管我们查询的是从 $i$ 到 $j$ 的一个区间，但是 $1$ 到 $i$ 的区域其实是未曾更新的！它们都是 $-\infty$。也就是说，只管查询 $j$ 的前缀最大值，与查询 $i$ 到 $j$ 是等价的。

注意一个细节！这里我调了好久才发现。 就是，$i+T_i$ 未必同余 $i$，那么它们各自的编号不能直接除，也就是不能查询 $\lfloor{\frac{(i+T_i)}{K}}\rfloor$。举个例子，当 $i=2933,K=20,T_i=44$ 的时候，$i+T_i$ 处于的块是 $99$，$i$ 则是 $97$。但实际上 $i+T_i$ 和 $i$ 的相对距离应该是 $\lfloor\frac {T_i}K\rfloor=1$。

这里我的解决方法大概是这样的，写一个 pos 函数：

int pos(int x,int y) {int tmp=x/K*K+y; while(tmp>x) tmp-=K; return tmp/K;}

问题 2

如果 $i$ 逐渐减小，发现无法快速维护。使用一个小 trick。

我们从 $i$ 开始遍历以后的块，发现它的 $-f(x)$ 情况就是 $0,-D,-2D,\dots$，也就是一个等差数列，第 $i$ 项和第 $i+1$ 项的差是 $D$。只要两两之间的差不变，它们的大小关系都不会变。因此我们弄一个新的等差数列，它的第 $i$ 项和第 $i+1$ 项的差也是 $D$，查到的数的位置铁定没毛病。

一个最简单的符合这个规律的数列就是：$\{\dots,i\cdot D,(i-1)D,\dots,2D,D,0\}$，也就是一个后缀形式的数列，很符合我们 dp 的形式。

当插入一个新的块的时候，如果这个块 $p_i$ 是 $i\equiv q \pmod K$ 这一类块中第 $j$ 个要插入的，插入树状数组时，加上 $(j-1)D$ 再插入。

假设当前 dp 到了 $i$，系数是 $c$，那么查询的实际答案就是 ${\rm query}(i)-c\cdot D$。

问题 3

类比问题 1，对全局再维护一个关于 $dp$ 的前缀树状数组 $\rm ALLBIT$。每次查询得到的答案减去 $f(j)$（这里 $f(j)$ 显然可以快速得出），即为这一段的贡献。假如答案在前面的整段，这里查出来的一定被前面的覆盖（$\max$ 操作有覆盖性），如果在这一段，得到的答案就是对的。

问题 4

$\rm BIT$ 的维护上文已经给出。

对于 $p$，我们显然不能暴力，不然会退化至 $O(nK)$。要维护加入、删除、查询最大值，std::set 也是一个选择，可惜常数太大，可能过不了。

但是！发现维护的区间长度是一定的！！！想到什么了吗？滑动窗口！

因此对于 $p$，单调队列一遍就行了！维护单调队列 $\rm queue$：

至此，问题终。总结一下过程：

程序实现

Solution1

方法二

如果你只想用树状数组而不想用单调队列，就试试这个方法吧。这个方法是听别人讲的，这里不再详述。

这一次，我们不像方法一，块不再移动了。固定分块！还是分 $O(K)$ 块，每块大小 $O(\frac nK)$。

对于一个余数 $i$ ，每一块都由两部分组成：$0$ 到 $i-1$ 一部分，$i$ 到 $K-1$ 一部分。每个部分内部的关于 $D$ 的增量相同，两个部分关于 $D$ 的增量差是 $D$。

我们发现，这次一段由三个部分组成：一段前缀，中间一段块，一段后缀。前缀可以直接用数组 $O(n)$ 记下（树状数组也行）。后缀一个树状数组，方法类似上文。

中间的处理是，对每一个余数开一个树状数组，大小为 $O(\frac nK)$。然后树状数组的第 $i$ 位表示第 $i$ 块的最大答案，这是可以线性求的。加入时的处理方法与方法一一样，增加一个公差为 $D$ 的等差数列，然后查询时减去。

程序实现

Solution2

方法三

这个，可以见这篇文章：https://www.luogu.com.cn/blog/six-floor-slip-liu/c0426-ban-yun-ji-ti-xie。

还有一个做法是单调栈，我不太会。